Convoy의 데이터과학팀은 빈도주의의 실험방법론이 product 혁신에 이상적이지 않는다고 생각합니다. 그래서 베이지안 통계를 사용하는 A/B 테스트 프레임워크로 바꾸었습니다. 왜냐하면, 더빨리 혁신하고 향상하는 것을 가능하게 해주기 때문입니다. 주어진 연속적으로 반복의 use case를 통해 베이지안 A/B 테스트가 위험과 속도의 균형을 잘 유지한다는 것을 알았습니다.
새로운 변수들이 적은 실험에서 베이지안 방법론은 이 새로운 변수들을 받아들일 수 있습니다. 많은 실험 과정에 걸쳐 베이지안 AB테스트를 사용함으로써 점진적인 개선을 얻는 것을 가속할 수 있습니다. 베이지안 A/B 테스트는 거짓양성비율(false positive rate : 1종 오류(type I error), 실제로는 음성인데 양성이라고 나오는 비율) 대신에 나쁜 결정에 대한 정도를 제어함으로써 신뢰성에 대한 희생 없이 개선을 성취할 수 있습니다.
이 글에서는 실험에 대한 기본사항들을 다루고, 베이지안 A/B 테스트의 이점을 소개하고, 이를 효과적으로 사용할 수 있는 미묘한 차이들에 대해서 논의할 것입니다.
실험 배경
어떤 A/B 테스트에서 각각의 변형에 대한 어떤 측정 항목(예시. 버튼을 클릭한 비율)을 계산하기 위해 A와 B의 변수들로부터 수집된 데이터를 사용합니다.
빈도주의 방법(Frequentist method)
빈도주의의 A/B 테스트에 우리는 두 가설(영가설 - A와 B 사이에 다른 점이 없다, 대립가설 : B는 다르다) 을 선택하기 위해 p-value를 사용합니다. 두 변수들 간에 차이가 없다고 주어졌을 때, p-value는 실제로 관찰한 것만큼 극적인 두 변수들 간의 차이를 관측한 확률을 측정합니다. p-value가 유의하거나 충분한 데이터를 얻으면 실험을 마치게 됩니다.
** 역자 주) 여기서 말하는 빈도주의 방법(Frequentist method)은 일반적인 영가설에 대한 통계적 유의성 검증을 의미하며, 이 포스트에서 빈도주의 방법은 일반적인 영가설 검증으로 이해하시면 될 것 같습니다.
베이지안 방법들
베이지안 A/B 테스트에서는 어떠한 확률 분포를 따르는 랜덤 변수로서 각각의 변수들에 대한 metric을 모델링합니다. 사전 경험(prior)을 기반으로 웹사이트의 전환율이 가능한 값의 어떤 범위에 있다고 믿습니다.
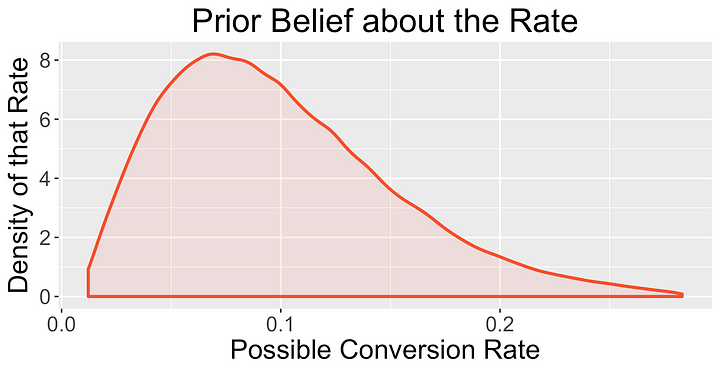
두 변수들로부터 데이터를 관측한 후에는 우리는 사전 믿음(prior)을 각 변수에 대해 가장 가능성이 있는 값으로 업데이트합니다. 아래에서 데이터를 관측하고 난 후에 사후분포(posterior)가 어떻게 바뀌는지에 대한 예시를 보여줍니다.
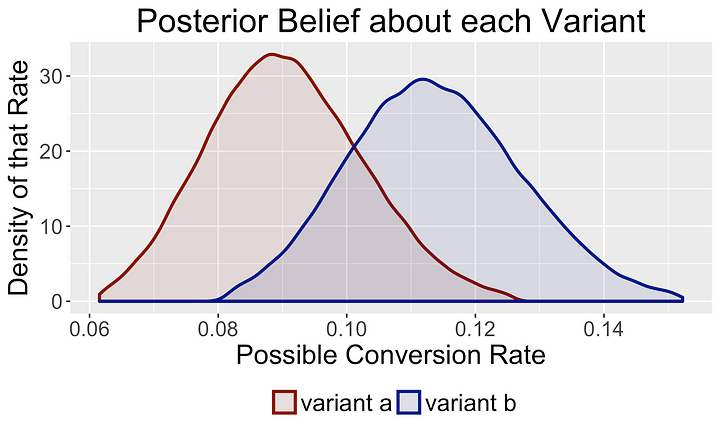
각 변수들에 대한 사후 분포(posterior)를 계산함으로써 확률론적인 표현을 통해 우리의 믿음에 대한 불확실성을 표현할 수 있습니다. 예를 들어, “변수 B에서의 metric과 변수 A에서 metric 중에서 확률이 더 큰 것은 무엇입니까?” 라고 물어볼 수 있습니다. 해석 가능한 결과는 데이터 과학자들이 모호한 상황에서 다른 동료들과 함께 최적 비즈니스 결정에 대한 생산적인 토론을 할 수 있도록 도와줍니다.
베이지안 A/B 테스트가 어떤 변수가 더 나은지 결정하기 전에 빈도주의 방법(Frequentist method)으로 만족스러운 솔루션을 제공하기 위해 노력하는 시나리오를 제공하고자 합니다.
빈도주의 방법(Frequentist method)들의 문제 : 아주 약간 나은 모델
빈도주의 방법의 문제점 중 하나는 영가설을 불필요하게 승인할 수 있다는 것입니다. 예를 들어, 데이터 과학자가 새로운 버전의 모델을 테스트하는 실험을 하고 싶다고 상상해보십시오. 충분한 데이터를 관찰한 결과 새로운 모델은 현재의 모델보다는 조금 나아졌으며, p-value는 0.11로 나타났습니다. 빈도주의 방법에서 시나리오의 적절한 절차는 현재의 모델을 유지하는 것입니다. 그러나 새로운 모델이 현재 모델보다 더 나은 예측을 하고 있기 때문에 이 결정은 매우 불만족스러우며, 잠재적인 비용이 많이 듭니다.
물론 처치(treatment : 실험계획법에서 각 실험단위에 가하는 특정실험조건)변수가 통제변수보다 약간 좋을 때 영가설을 고수하기를 원하는 시나리오도 있습니다. 만약에 처치 변수에 많은 엔지니어링 유지보수가 필요하거나 사용자 환경(UX)에 지장을 초래한다면 새 변수를 구현하는 비용이 (새 변수를 구현함으로써 얻는) 작은 이점보다 클 수가 있습니다. 그러나 Convoy에서의 경험에 의하면 이러한 시나리오는 흔하지 않습니다.
약간 더 나은 모델의 경우와 비슷한 시나리오에서, 베이지안 방법론은 약간 개선된 변수를 허용하기 때문에 매력적입니다. 향후 몇 년 동안 동일한 핵심 비즈니스 지표에 대해서 수백 가지 실험을 수행한다면 한계이익이 차곡차곡 쌓일 것입니다.
작은 개선을 제공하는 변수를 허용함으로써 베이지안 A/B테스트는 거짓양성비율(처치가 약간 더 나을 때 처치를 받아들일 수 있는 횟수의 비율)이 중요하지 않다고 주장합니다. 일부 통계학자들에게는 충격적일지 모르겠지만 모든 거짓양성반응이 동등하게 생성되는 것이 아니기 때문에 이 문장에 동의합니다.
대신 베이지안 A/B 테스트는 많은 실험들에 대해 잘못된 결정의 평균적인 정도에 초점을 맞춥니다. 당신의 결정이 product를 실제로 나쁘게 만들 수 있는 평균금액을 제한함으로써 metric의 장기적인 개선에 대한 보장을 제공합니다. Convoy의 데이터과학팀은 이러한 (장기적인 개선에 대한) 보장이 빈도주의 방법의 거짓양성비율에 대한 보장보다 Convoy의 Use case에 훨씬 더 관련이 있다고 믿습니다.
베이지안 방법론
이 섹션에서는 베이지안 A/B 테스트가 의사결정을 내리는 방법과 장기적인 개선을 보장하는 방법을 설명합니다. 이 방법론은 Chris Stucchio의 백서에서 나온 것입니다.
α, β는 A, B 변수에 대한 근본적이고 관찰되지 않은 실제 척도를 나타냅니다. x는 우리가 선택한 변수를 나타냅니다. 그러면 우리는 손실 함수를 다음에 주어진 실험에서처럼 정의할 수 있습니다.
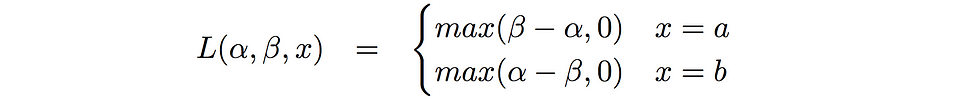
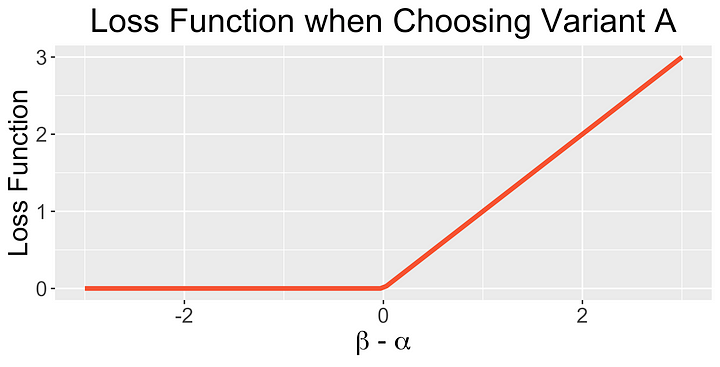
여기서 우리는 변수 A를 β-α의 함수로써 선택하는 손실을 시각화합니다.
만약 α가 β보다 작을 때, 변수 A를 선택하면 손실이 β-α가 됩니다. α가 β보다 크다면 우리는 아무것도 잃지 않습니다. 손실은 우리가 변수를 선택할 때 metric이 감소하는 양입니다.
왜냐하면, α와 β의 참 값을 관찰 할 수 없기 때문에, 우리는 결합 사후 밀도 함수 f(α, β)에 대한 기대 손실을 계산합니다.
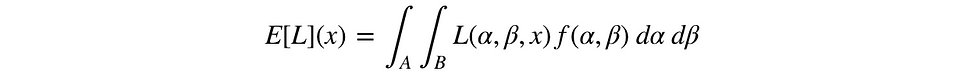
변수들 중 하나에 대한 기대 손실이 어떤 임계값 ε 이하로 떨어지면 실험을 중단합니다. 우리는 그 변수를 선택하는 것이 좋은 비즈니스 결정이라고 결론을 내릴 충분한 증거가 있습니다.
이 중지 조건은 β-α가 0보다 클 가능도(likelihood)와 이 차이의 크기를 모두 고려합니다. 결론적으로, 매우 중요한 두 가지 속성입니다 :
- 다른 정도의 오차를 다르게 다룹니다. 만약에 α와 β의 값이 불확실하다면 큰 실수를 범할 가능성이 더 커집니다. 결과적으로 기대 손실도 더 커집니다.
- 어떤 변수가 더 큰지 확실하지 않은 경우에도 변수 간의 차이가 작은 것으로 확인되는 순간 테스트를 중단할 수 있습니다. 이 경우 오류가 있다면(예 : β <α 일때 β를 선택함), 오류의 정도가 작아지는 것을 확신할 수 있습니다(β = 10%, α = 10.1%). 결과적으로는 우리의 결정이 우리의 metric을 크게 감소시키지 않을 것이라고 확신할 수 있습니다.
방법론에 대한 이해
변수에 대한 기대손실은 변수를 선택하면 metric이 감소하는 평균 크기이기 때문에 그 평균 크기의 오차를 편하게 할 만큼 ε이 너무 작게 설정해야 한다. 이 아이디어는 오히려 ε 크기의 오차를 만듭니다. 그리고 첫 번째 실험에 너무 많은 시간을 보내기보다 또 다른 유망한 실험으로 이동하게 만듭니다.
ε에 대해서 더 잘 이해하고 베이지안 A/B 테스트의 보장에 대한 증거를 보려면 몇 가지 시뮬레이션을 실행해보는 것이 좋습니다. 250개의 실험을 고려해보십시오. 각 실험에서 두 변수 중 하나의 기대 손실이 ε 아래가 되면 실험을 중단합니다. 모든 실험에서 α와 β의 실제 값은 위에 제시된 사전 분포로부터 독립적으로 추출된다고 가정합니다.
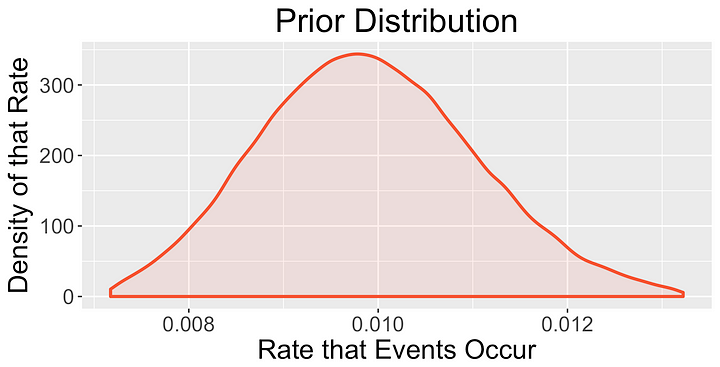
일단 모든 실험이 끝나면, 평균 관측 손실을 계산하기 위해 α와 β의 실제 값을 사용합니다. 많은 다른 값의 ε에 대해 이 과정을 반복하면 아래의 그림과 같은 결과를 얻습니다(github의 Script로부터 복사해온).
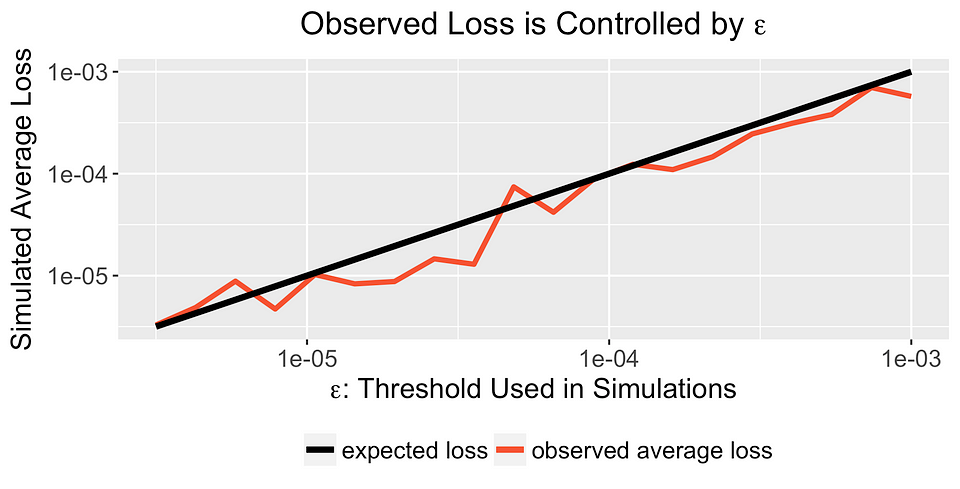
이 그래프는 베이지안 A/B 테스트가 제공하는 보장을 보여줍니다. 실험을 중단하면 평균적으로 metric을 ε만큼 줄이는 결정을 내리지 않을 것이라고 확신할 수 있습니다. 실험에서 (또다른) 실험까지 metric이 꾸준하게 증가하기 때문에 이러한 보장은 빠르게 (실험을) 반복하고 관측할 수 있게 해줍니다.
데이터를 최대한 활용하기
사전분포 선택의 타당함을 보이기
베이지안 분석의 비평가들은 사전 분포의 선택이 충분히 타당하지 않았다는 것으로 주장할 수 있습니다. 사실, 이전 섹션에서 제시한 시뮬레이션은 완벽한 사전 분포를 사용한다고 가정합니다.
다행히 A/B 테스트를 지속적으로 실행하는 회사의 경우 대개 풍부한 사전 정보가 있습니다. Convoy가 A/B 테스트에서 모니터링하는 metric은 회사 전체에서 사용되는 주요 성과 지표입니다. 주간 평균 데이터나 과거 실험결과를 검토함으로써 metric이 취할 수 있는 값 범위를 잘 이해할 수 있습니다.
결론에 빨리 도달하기
관련된 사전 정보를 사용하면 실험이 더 빨리 끝납니다. 사전 (분포)에 집어넣은 모든 정보는 우리가 데이터로부터 배울 필요가 없는 정보입니다. 베이지안 A/B 테스트는 사전분포를 활용함으로써 결론에 도달하는 데 필요한 데이터 포인트가 더 적을 수 있습니다.
예를 들어 베르누이의 사전분포로써 베타(1,1)을 사용한다고 가정해봅시다. 40번의 성공과 60번의 실패를 관찰한 결과 우리의 사후분포는 베타(41,61)입니다. 그러나 베타(8,12)를 사전 분포로 실험을 시작한 경우라면 이전과 동일한 분포를 얻기 위해 32번의 성공과 48번의 실패만을 관찰하면 됩니다.
관찰된 모든 데이터를 압도할 수 있을만큼 강력하지 않은 사전 분포는 사용하지 않는 게 좋습니다. 역사적으로 데이터가 암시하는 것보다 약한 사전 분포를 선택하는데 있어 일반적으로 좋은 습관입니다.
각주
- 일반적으로 우리는 95%의 통계적 유의성 또는 80%의 의사 결정력이 나올 만큼 충분한 데이터가 나올 때까지 기다립니다.
- 연속적으로 관찰되는 문제를 피하기 위해 순차 분석을 사용할 수 있습니다.
- 샤이니앱을 사용하여 동료가 데이터와 베이지안 테스트를 알게 할 수있습니다.
- 베이지안 A/B 테스트는 (손실함수에 대한) 비용을 직접 계량할 수 있습니다. 자세한 내용 Appendix를 참조하십시오.
- Conjugate Prior를 사용한다고 가정할 때, 이러한 계산에 대한 분석적인 공식이 있습니다.
참고자료
The Power of Bayesian A/B Testing by Jeremy Hermann (Data Scientist at Convoy building a automated marketplace for transportation.)
The work done by Chris Stucchio and Evan Miller was instrumental in our adoption of a Bayesian A/B testing framework. I also found David Robinson’s post very helpful when reading other evaluations of Bayesian A/B testing.
Appendix
영가설에 대한 Bias
우리가 통제변수와 처치변수들 간의 무차별(indifferent)이고 싶지 않은 상황이 있다면 다행히도 베이지안 A/B 테스트의 손실함수는 사용자 정의가 가능합니다. 예를 들어 다음과 같이 작성할 수 있습니다 :
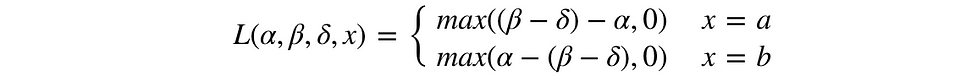
이 손실 함수에서, δ는 우리가 변수 B로 전환하기 위해 β가 α보다 좋을 필요가있는 양입니다. 각 실험에 대해 δ를 정량화 할 수 있으며 기본값은 δ = 0 입니다.