마케팅 캠페인들을 적극적으로 운영하는 비즈니스에서는 마케팅 채널들이 실제 전환을 유도하는지를 파악하는데 관심을 가져야 합니다. 마케팅 노력들에 대한 ROI(투자수익률)이 중요한 KPI인 것은 모두가 아는 사실입니다.
이 아티클에서는 다음 내용을 다룰 예정입니다.
- 채널별 기여(Attribution)가 중요한 이유가 무엇인지
- 3가지 기여 모델들
- 고급 기여 모델 : 마코프체인
- 파이썬에서 4가지 모델을 만드는 방법
왜 기여가 중요할까요?
기업들이 고객들에게 마케팅할 수 있는 다수의 플래폼들이 증가하고, 대부분의 고객들은 다양한 채널들을 통해 당신의 컨텐츠에 관여하고 있기 때문에 어떠한 채널들이 전환에 기여하는지를 결정하는 것은 무엇보다도 중요합니다. 2017년의 연구에 따르면 92% 소비자들은 처음 방문한 소매업체의 웹사이트를 구매하지 않는다고 합니다(링크).

기여의 중요성을 설명하기 위해 전환으로 이어지는 사용자의 여정의 간단한 예를 살펴보겠습니다. 이 예에서 사용자의 이름은 John 입니다.
첫째날 : 귀하의 제품에 대한 John의 인식은 YouTube 광고에 의해 시작되어 귀하의 웹사이트를 방문하여 귀하의 제품 카탈로그를 검색하게 됩니다.
약간의 브라우징 후에 귀하의 제품에 대한 John의 인식이 생겼지만 구매까지 완료할 의사는 발생하지 않았습니다.
둘째날 :
다음날 John이 Facebook 피드 스크롤링 하면서 귀하의 제품에 대한 또다른 광고를 수신하게 됩니다. 이 광고는 귀하의 웹사이트로 돌아가도록 권유하고 John은 이번에는 구매 프로세스를 완료합니다.
이러한 경우에 마케팅 채널로부터의 ROI를 계산하려고 할 대 어떠한 마케팅 채널을 통해 John이 생성한 전환 금액이 어떻게 기여되었는지를 나타낼 수 있습니까?
전통적으로 채널 기여는 퍼스트 터치, 라스트 터치 및 선형과 같은 간단하면서도 강력한 접근 방식이 사용되었습니다.
표준 기여 모델들
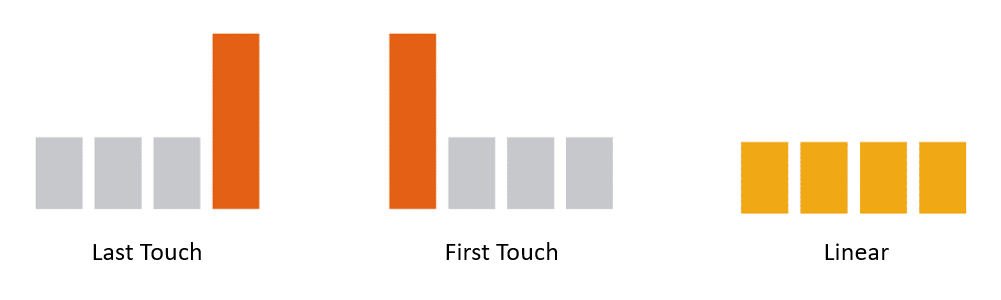
라스트 터치 어트리뷰션(Last Touch Attribution)
이름에서 알 수 있듯이 라스트 터치는 발생한 수익이 사용자가 마지막에 접근한 마케팅 채널에서 기여되었다고 보는 기여 방법입니다.
이 방식은 단순성 측면에서는 장점이 있지만 마지막 터치가 반드시 구매를 창출하는 마케팅 활동일 필요가 없으므로 기여를 지나치게 단순화할 위험이 있습니다.
위의 John의 예시에서 마지막 터치 채널(페이스북)은 구매 의도의 100%를 만들지 않았을 가능성이 큽니다. 이러한 인식은 Youtube 광고를 보았을 때 처음 발현된 것입니다.
퍼스트 터치 어트리뷰션(First Touch Attribution)
구매로 인해 발생한 수익은 구매를 향한 여행에서 사용자가 참여한 첫번째 마케팅 채널로부터 발생한 것입니다.
라스터 터치 방식과 마찬가지로 퍼스트 터치 어트리뷰션은 단순성 측면에서는 장점이 있지만 마찬가지로 기여 방법을 지나치게 단순화하는 위험이 있습니다.
선형 어트리뷰션(Linear Attribution)
이 방식에서는 구매로 이어지는 여정 동안에 사용자가 터치한 모든 마케팅 채널에 균등하게 기여가 분할 됩니다.
이 방법은 소비자 행동에서 볼 수 있는 다중 채널 터치 동작의 추세를 파악하는데 더 적합합니다. 그러나 채널들 간의 차이를 구별하지 않으며 모든 소비자가 마케팅 노력들에 대해 동등하게 참여하지 않기 때문에 이 모델은 분명한 단점이 있습니다.
다른 표준 기여 방법들을 언급하자면 Time Decay Attribution과 Position Based Attribution이 있습니다(참고자료의 구글애널리틱스 기여모델을 참고하세요)
진보된 기여 모델 : 마코프 체인(Makov Chain)
위의 세가지 기여 모델들을 통해 마케팅 채널의 ROI를 파악하기 쉬운 모델을 구현할 수 있습니다.
그러나 이러한 3가지 모델들에 대해 주의할점은 지나치게 단순화되어 있다는 점입니다. 이 것은 마케팅 채널로 부터 발생된 결과(전환 or 수익)에 대한 과신을 야기할 수 있습니다. 이러한 불찰은 미래의 비즈니스/마케팅 결정들을 해로운 방향으로 잘못 이끌 수 있습니다.
이 불찰을 극복하기 위해 우리는 보다 진보된 기여 모델인 마코프 체인을 고려할 수 있습니다.
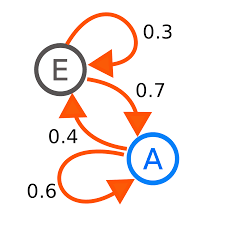
통계 과정을 수강했다면 이 이론을 접했을 수 있습니다. 마코프 체인은 러시아의 수학자인 마르코프의 이름을 따서 지어졌으며 각 사건의 확률이 이전 사건에 얻어진 상태에만 의존하는 일련의 가능한 사건들을 말합니다.
채널 기여의 맥락에서 마코프 체인은 사용자의 여정을 모델링하는 프레임워크(마코프 체인의 상태 전이도)와 사용자들이 최종구매가 일어날 때까지 각각 한 채널에서 또다른 채널로 이동하게 되는 지수(마코프 체인의 상태 전이 확률)를 제공합니다.
우리는 이 기사에서 마코프 체인의 이론을 깊이 있게 들어가지 않을 것입니다. (배경지식에 필요한 수학/통계를 깊이 알고 싶다면 Setosa.io를 잘 읽어보세요.)
마코프 체인의 핵심 개념은 생성된 데이터를 한 채널에서 네트웍 상의 또 다른 잠재적인 마케팅 채널로 이동할 확률 식별하는데 사용할 수 있다는 것입니다.
다음 섹션에서 이러한 기여 프레임워크를 실행하기 위한 파이썬 코드를 살펴보도록 하겠습니다.
파이썬으로 네가지 기여모델을 만드는 방법
따라하기를 원한다면 이 예제에서 사용할 데이터 셋을 여기에서 다운로드할 수 있습니다.
이 데이터 셋은 (마케팅 채널의) 참여 활동이 열로 행은 참여 채널로 시간 순서대로 구성되었습니다. 만약 한 유저가 n번째 마케팅 채널에 참여했다면 각각의 마케팅 채널은 n번째 보이는 고정된 값에 할당됩니다. 채널 21은 전환이며 데이터 셋에서 사용자의 여정이 전환된 결과만을 포함하게 됩니다.

우리가 할 첫번째 일은 필요한 라이브러리들을 불러오는 것입니다.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import subprocess다음에는 데이터 셋을 로드하고 정리합니다.
# Load in our data
df = pd.read_csv('Channel_attribution.csv')
# Grab list of columns to iterate through
cols = df.columns
# Iterate through columns to change all ints to str and remove any trailing '.0'
for col in cols:
df[col] = df[col].astype(str)
df[col] = df[col].map(lambda x: str(x)[:-2] if '.' in x else str(x))마코프 체인 프레임워크는 단일 변수와 채널1 > 채널2> 채널3 > … 형태로의 사용자 여정을 원하기 때문에 아래와 같이 다음 루프를 정확하게 생성합니다.
# Create a total path variable
df['Path'] = ''
for i in df.index:
#df.at[i, 'Path'] = 'Start'
for x in cols:
df.at[i, 'Path'] = df.at[i, 'Path'] + df.at[i, x] + ' > '데이터 셋의 채널 21은 전환 사건이므로 경로에서 해당 채널을 분리하고 발생하는 전환 수를 별도의 전환 변수로 만듭니다(사용자의 여정 레벌 데이터가 1개일때만)
# Split path on conversion (channel 21)
df['Path'] = df['Path'].map(lambda x: x.split(' > 21')[0])
# Create conversion value we can sum to get total conversions for each path
df['Conversion'] = 1이제 초기 데이터 작업은 완료되었습니다. 데이터에는 여전희 원래의 모든 열들이 포함되어 있으므로 앞으로 필요한 하위집합(subset)만 가져오도록 합니다. 일부 사용자들은 동일한 여정을 했으므로 고유한 사용자의 여정으로 데이터를 그룹화하고 전환 변수에서는 각 여행에 대한 전환 수가 저장됩니다.
# Select relevant columns
df = df[['Path', 'Conversion']]
# Sum conversions by Path
df = df.groupby('Path').sum().reset_index()
# Write DF to CSV to be executed in R
df.to_csv('Paths.csv', index=False)
The last line in the above piece of code will위의 코드의 마지막 줄은 데이토 조작을 완료한 데이터를 csv 파일로 출력합니다. 투명성 목적으로 이 데이터를 사용하는 것이 편리합니다. 우리의 경우에는 마코프 체인 기여 모델을 실행하기 위해 이 csv 파일을 사용할 것입니다.
이를 수행하는 몇 가지 방법이 있습니다. 파이썬은 현재 이를 만들기 위한 라이브러리가 없기 때문에 실제로 파이썬에서 마코프 체인/네트워크를 스스로 구축하는 것이 좋습니다. 이렇게 하면 모델에 대한 개요를 볼 수 있지만 시간이 많이 소요되는 방법이기도 합니다. 우리는 보다 효율적으로 단일 어플리케이션으로써 마코프 체인에 집중된 이론을 가진 R 라이브러리인 ChannelAttribution을 사용하려고 합니다.
표준 파이썬 라이브러리를 서브 프로세스를 사용하여 마코프 네트워크를 계산하는 다음과 같은 R 코드를 실행합니다.
# Read in the necessary libraries
if(!require(ChannelAttribution)){
install.packages("ChannelAttribution")
library(ChannelAttribution)
}
# Set Working Directory
setwd <- setwd('C:/Users/Morten/PycharmProjects/Markov Chain Attribution Modeling')
# Read in our CSV file outputted by the python script
df <- read.csv('Paths.csv')
# Select only the necessary columns
df <- df[c(1,2)]
# Run the Markov Model function
M <- markov_model(df, 'Path', var_value = 'Conversion', var_conv = 'Conversion', sep = '>', order=1, out_more = TRUE)
# Output the model output as a csv file, to be read back into Python
write.csv(M$result, file = "Markov - Output - Conversion values.csv", row.names=FALSE)
# Output the transition matrix as well, for visualization purposes
write.csv(M$transition_matrix, file = "Markov - Output - Transition matrix.csv", row.names=FALSE)다음의 파이썬 코드는 R 스크립티를 실행하고 csv 파일로 결과를 로드합니다.
# Define the path to the R script that will run the Markov Model
path2script = 'C:/Users/Morten/PycharmProjects/Markov Chain Attribution Modeling/Markov.r'
# Call the R script
subprocess.call(['Rscript', '--vanilla', path2script], shell=True)
# Load in the CSV file with the model output from R
markov = pd.read_csv('Markov - Output.csv')
# Select only the necessary columns and rename them
markov = markov[['channel_name', 'total_conversion']]
markov.columns = ['Channel', 'Conversion']마코프 체인 계산을 실행하기 위해 별도의 R 스크립트를 작성해야 하는 경우, 사용할 수 있는 파이썬 라이브러리는 ‘rpy2’입니다. ‘rpy2’를 사용하면 R 라이브러리를 가져와서 파이썬으로 직접 호출할 수 있기 때문입니다. 그러나 이 방법은 프로세스 동안 안정적이라는 것이 증명되지 않았기 때문에 별도의 R 스크립트 접근 방법을 선택했습니다.
마코프 체인을 사용한 채널의 기여도는 아래 차트에서 확인할 수 있습니다. 이 차트에서 20번 채널에서 매우 많은 전환이 발생하고 18번 채널과 19번 채널은 총 전환 가치가 매우 낮은 것으로 확인되었습니다.
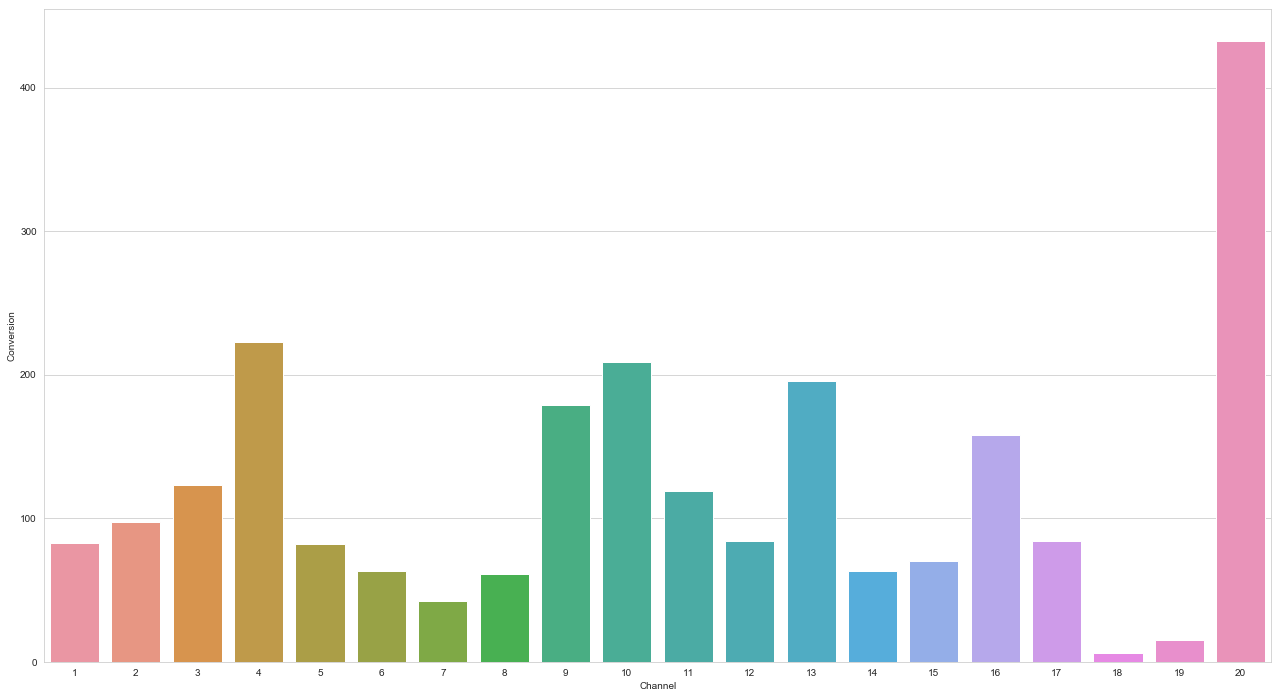
당신이 찾고 있는 것이 이 산출물(마코프 체인을 사용한 기여도 평가)일 수도 있지만 전통적인 모델들의 산출물이 마코프 체인 모델과 비교하여 어떻게 생겼는지에 대한 정보도 많은 가치가 있습니다.
라스트 터치, 퍼스트 터치 및 선형에 대한 속성을 계산하기 위해 다음 코드를 실행합니다.
# First Touch Attribution
df['First Touch'] = df['Path'].map(lambda x: x.split(' > ')[0])
df_ft = pd.DataFrame()
df_ft['Channel'] = df['First Touch']
df_ft['Attribution'] = 'First Touch'
df_ft['Conversion'] = 1
df_ft = df_ft.groupby(['Channel', 'Attribution']).sum().reset_index()
# Last Touch Attribution
df['Last Touch'] = df['Path'].map(lambda x: x.split(' > ')[-1])
df_lt = pd.DataFrame()
df_lt['Channel'] = df['Last Touch']
df_lt['Attribution'] = 'Last Touch'
df_lt['Conversion'] = 1
df_lt = df_lt.groupby(['Channel', 'Attribution']).sum().reset_index()
# Linear Attribution
channel = []
conversion = []
for i in df.index:
for j in df.at[i, 'Path'].split(' > '):
channel.append(j)
conversion.append(1/len(df.at[i, 'Path'].split(' > ')))
lin_att_df = pd.DataFrame()
lin_att_df['Channel'] = channel
lin_att_df['Attribution'] = 'Linear'
lin_att_df['Conversion'] = conversion
lin_att_df = lin_att_df.groupby(['Channel', 'Attribution']).sum().reset_index()4가지 모델들과 모델들의 산출물의 차이점을 함께 평가해봅시다.
# Concatenate the four data frames to a single data frame
df_total_attr = pd.concat([df_ft, df_lt, lin_att_df, markov])
df_total_attr['Channel'] = df_total_attr['Channel'].astype(int)
df_total_attr.sort_values(by='Channel', ascending=True, inplace=True)
# Visualize the attributions
sns.set_style("whitegrid")
plt.rc('legend', fontsize=15)
fig, ax = plt.subplots(figsize=(16, 10))
sns.barplot(x='Channel', y='Conversion', hue='Attribution', data=df_total_attr)
plt.show()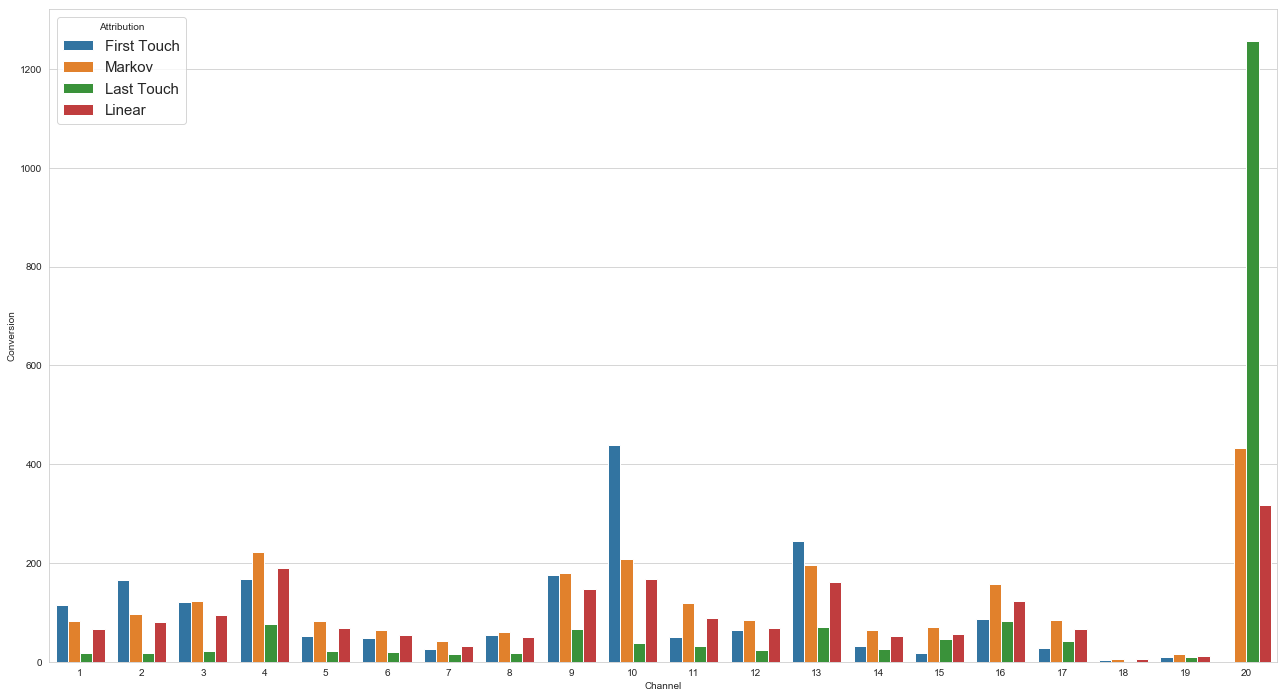
위의 차트를 보면 대부분의 사용자의 여정은 채널 10에서 시작하여 채널 20으로 끝나고 채널 20에서는 사용자의 여정이 시작되지 않는다고 결론을 내릴 수 있습니다.
다른 채널이 잠재적인 사용자의 여정에 어떻게 영향을 미치는지에 대한 아이디어를 얻기 위해 우리는 전체 전이 행렬을 시각화한 히트맵을 살펴볼 수 있습니다.
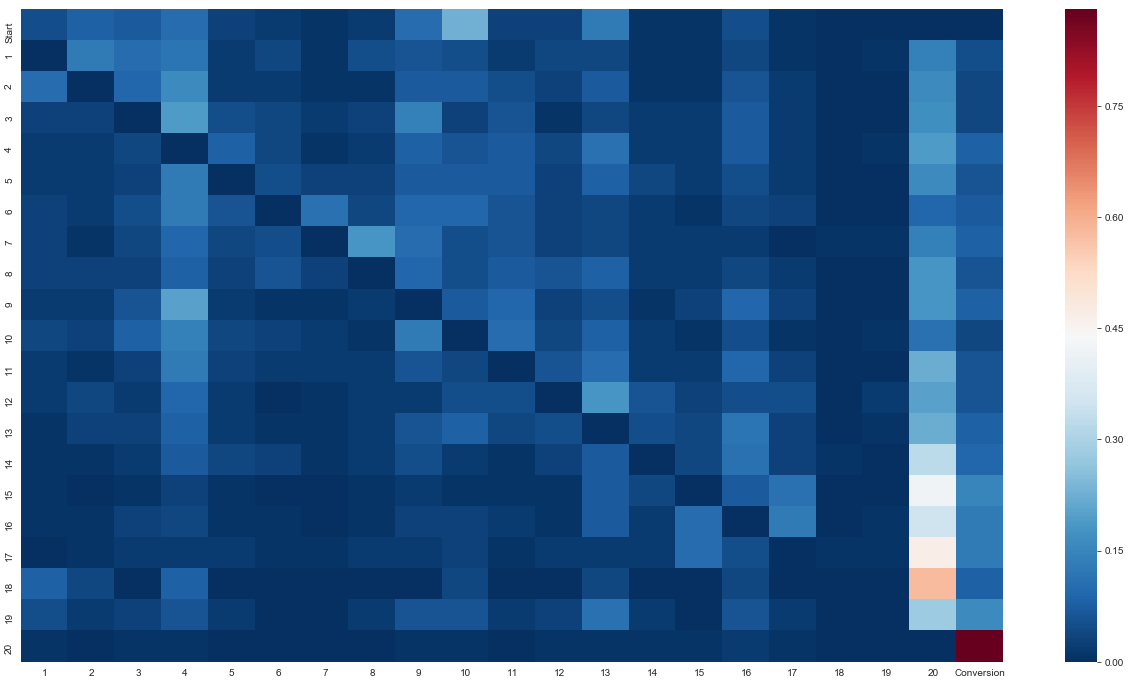
다음 코드를 실행하면 :
# Read in transition matrix CSV
trans_prob = pd.read_csv('Markov - Output - Transition matrix.csv')
# Convert data to floats
trans_prob ['transition_probability'] = trans_prob ['transition_probability'].astype(float)
# Convert start and conversion event to numeric values so we can sort and iterate through
trans_prob .replace('(start)', '0', inplace=True)
trans_prob .replace('(conversion)', '21', inplace=True)
# Get unique origin channels
channel_from_unique = trans_prob ['channel_from'].unique().tolist()
channel_from_unique.sort(key=float)
# Get unique destination channels
channel_to_unique = trans_prob ['channel_to'].unique().tolist()
channel_to_unique.sort(key=float)
# Create new matrix with origin and destination channels as columns and index
trans_matrix = pd.DataFrame(columns=channel_to_unique, index=channel_from_unique)
# Assign the probabilities to the corresponding cells in our transition matrix
for f in channel_from_unique:
for t in channel_to_unique:
x = trans_prob [(trans_prob ['channel_from'] == f) & (trans_prob ['channel_to'] == t)]
prob = x['transition_probability'].values
if prob.size > 0:
trans_matrix[t][f] = prob[0]
else:
trans_matrix[t][f] = 0
# Convert all probabilities to floats
trans_matrix = trans_matrix.apply(pd.to_numeric)
# Rename our start and conversion events
trans_matrix.rename(index={'0': 'Start'}, inplace=True)
trans_matrix.rename(columns={'21': 'Conversion'}, inplace=True)
# Visualize this transition matrix in a heatmap
sns.set_style("whitegrid")
fig, ax = plt.subplots(figsize=(22, 12))
sns.heatmap(trans_matrix, cmap="RdBu_r")
plt.show()결론
여러가지 마케팅 채널들에 대한 접근법은 각각 다른 비즈니스들에 적합합니다. 이 아티클에서는 마케팅 지출의 효과를 평가할 수 있는 4가지 방법을 설명했습니다. 우리는 과신으로 이어질 수 있는 당신의 데이터 구조에 관계 없이 적용할 수 있는 3가지 방법들을 알아보았습니다. 반면에 마코프 체인 방법은 사용자의 여정 데이터가 어떻게 구성되어 있는지를 고려하여 채널의 기여를 모델링합니다. 이 방법이 더 복잡하긴 하지만
마코프 체인 모델의 결과를 분석하면 특정 시점에서의 마케팅 채널 효과에 대한 스냅샷을 얻을 수 있습니다. 새로운 마케팅 캠페인 시작 전후의 데이터에 대한 모델의 결과물을 보고 캠페인이 각 채널의 실적에 어떻게 영향을 미치는 지에 대한 필수 정보를 제공하여 추가적인 인사이트를 얻을 수 있습니다.
보다 세분화된 기능을 추가하고 데일리 기여 모델을 운영함으로써 PCC 또는 마케팅 비용 지출들 간의 상관관계를 평가하고 상관 모델을 사용하여 채널 기여를 평가할 수 있습니다.
이 아티클에서 제시된 접근법은 복잡하게 추가하면 모델의 결과의 가치를 높일 수 있지만 실제 비즈니스 가치는 이러한 양적 모델들의 결과를 해석하고 이를 비지니스 도메인 지식과 당신의 데이터로부터 생산된 전략적인 비즈니스 계획과 결합하는 것으로부터 옵니다.
마케팅 채널 기여는 복잡한 임무가 될 수 있으며 소비자들이 이전보다 더 많은 마케팅에 도달하게 될 수 있습니다. 기술이 발전하고 더 많은 채널들에서 마케팅이 가능하게 되면서 가장 많은 ROI를 이끌어내는 채널이 정확히 어디인지 파악하는 것이 중요해지고 있습니다.
당신의 데이터로부터 귀중한 기여에 대한 정보를 어떻게 파악하고 있습니까?
참고자료
Marketing Channel Attribution with Markov Chains in Python by Morten Hegewald
구글애널리틱스 기여 모델(이 아티클에서 다루어진 내용 외의 블로그 내용을 여기에서 참고하세요.)