참고자료
Almost Everything You Need to Know About Time Series by Marco Peixeiro
금융시장의 트렌드를 예측하거나, 전력 소모량을 예측하든지 간에 시간은 이제 우리의 모델에서 반드시 고려되어야하는 중요한 요소입니다. 예를 들어 주가가 현재의 가격보다 상승할 지 아는 것 뿐 아니라, 언제 상승 할지까지 아는 것은 흥미로운 일입니다.
시계열 데이터를 한번 살펴봅시다. 시계열 데이터는 간단히 시간순으로 정렬된 데이터 포인트들입니다. 시계열 데이터에서 시간은 거의 독립적인 변수이고, 보통 시계열 데이터를 통해 미래를 예측하는 것을 목표로 합니다.
시계열을 다룰 때 작용하는 다음과 같은 특성들이 있습니다.
-
Stationary(고정적)인가?
-
Seasonality(계절성)이 있는가?
-
목표 변수가 autocorrelated(자기 상관) 인가?
이 글에서는, 시계열의 다른 특성들과 가능한한 정확한 예측을 얻기 위해 그것들을 우리가 어떻게 모델링할지 소개하려고 합니다.
Autocorrelation
일상적으로, autocorrelation은 관측치들간의 사이의 시간 지연 함수로서 유사성을 말합니다.
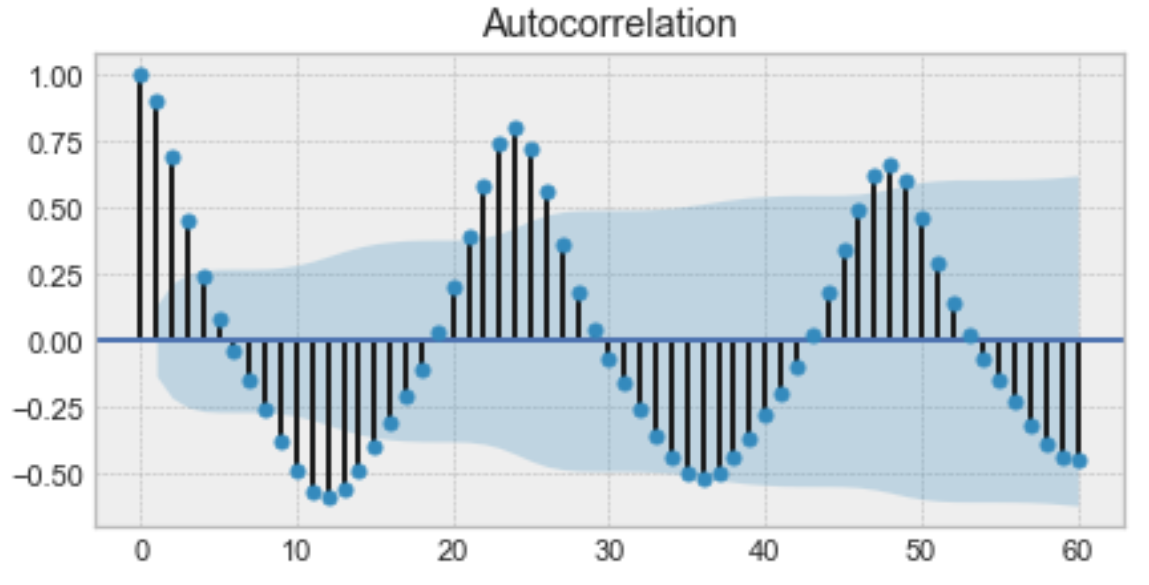 Autocorrelation 그래프의 예시
Autocorrelation 그래프의 예시
위는 autocorrelation 그래프의 한 예시입니다. 자세히보면, 당신은 첫번 째 값과 24번째 값이 높은 자기 상관 관계를 가진다는 것을 깨닫게 됩니다. 유사하게, 12번째 값과 36번째 값이 높은 자기 상관 관계를 가집니다. 이는 우리가 매 24 시간 단위 마다 매우 유사한 값을 발견할 수 있다는 것을 의미합니다.
그래프가 sinusoidal 함수와 유사함에 주목하세요. 이것은 계정성에 대한 힌트이며, 당신은 위의 그래프에서 24시간으로 주어진 기간을 찾아 값을 알아낼 수 있습니다.
Seasonality
Seasonality는 주기적인 변동을 의미합니다. 예를 들어, 전력 소모량은 낮 시간동안에 낮고, 저녁시간 동안에 높습니다. 그리고 온라인 판매량은 크리스마스 전에 증가하고 다시 감소합니다.
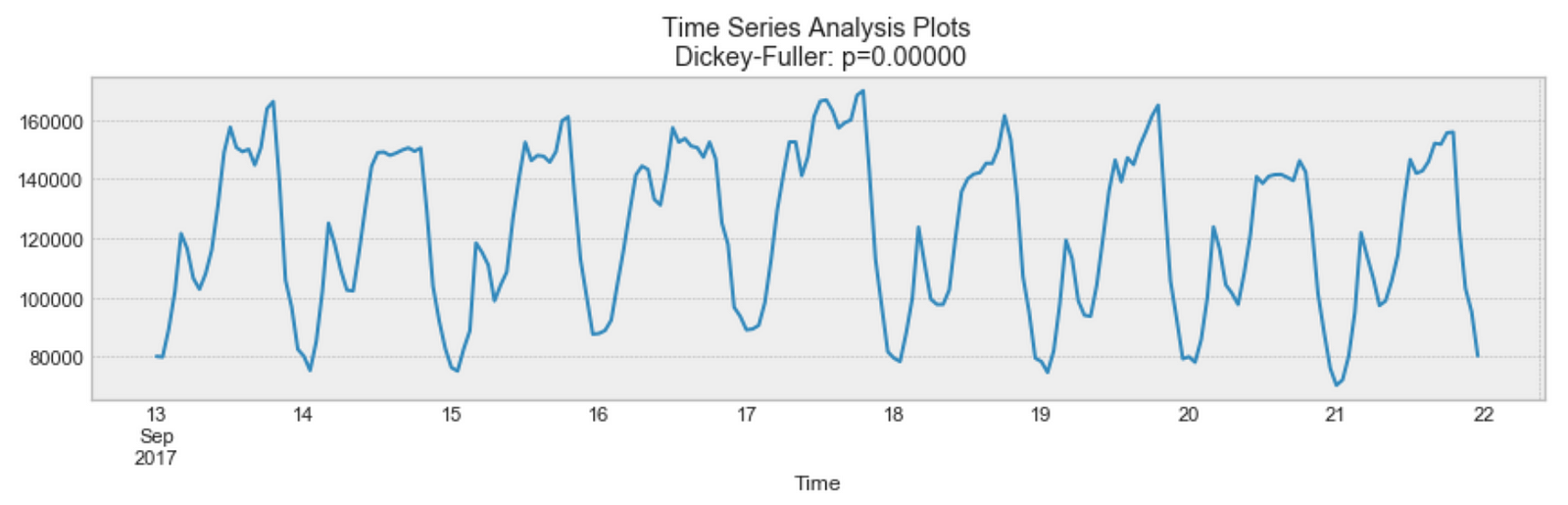 Seasonality의 예
Seasonality의 예
위 예시에서 볼 수 있듯이, 위 그래프에서는 일별 seasonality가 명확하게 드러나 있습니다. 매일 밤으로 갈수록 최고점에 도달하고, 가장 최저점은 매일의 시작과 끝에서 나타납니다.
seasonality는 또한 sinusodial 모양을 가진 autocorrelation 그래프에서도 도출될 수 있음을 기억하세요. 단순히 주기를 보는 것만으로, seasonality의 길이를 알 수 있습니다.
Stationarity
Stationarity은 시계열 데이터에서 중요한 특성입니다. 시계열 데이터가 stationary 라는 것의 의미는 해당 데이터의 통계적 성질이 시간이 지남에 따라 변하지 않는 경우를 의미합니다. 다른 말로, 시간에 독립적으로 고정적인 평균과 분산, 공분산 값을 가진다는 것을 말합니다.
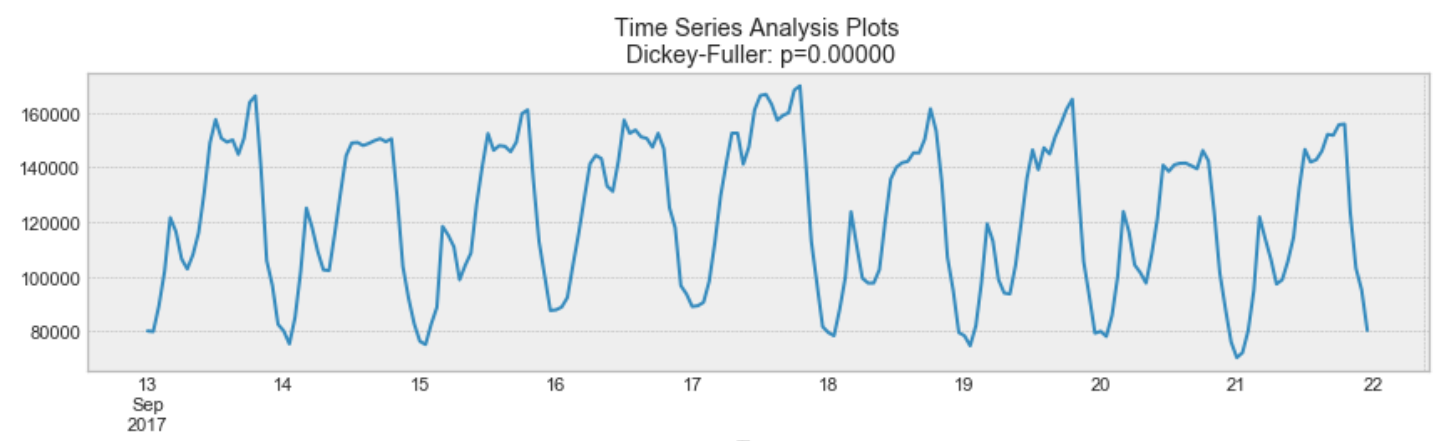 Stationary Process의 예
Stationary Process의 예
위에서 나온 그래프를 다시 보면, 위의 그래프가 stationary임을 알 수 있습니다. 평균과 분산이 시간이 지남에 따라 변하지 않습니다.
종종 주식 가격은 stationary 하지 않고, 아마 시간이 지남에 따라 진화하는 트렌드를 보거나 변동성이 증가하는 (분산이 변화하는) 것을 볼 수 있을 것입니다.
이상적으로, 우리는 모델링을 위해서는 stationary 특성을 가진 시계열 데이터를 원합니다. 물론, 모든 시계열 데이터가 stantionary 하지는 않지만 우리는 그러한 데이터들을 다르게 변형하여 stantionary 하도록 만들 수 있습니다.
How to test if a process is stationary
당신은 아마 위의 그래프의 제목에 있는 Dickey-Fuller 라는 단어를 발견했을 수 있습니다. Dickey-Fuller는 어떤 시계열 데이터가 stationary인지 아닌지 판단하기 위해 사용하는 통계 테스트입니다.
Dickey-Fuller 검증 테스트(참고)에서
- p > 0 인 경우 stationary 데이터가 아닙니다.
- p = 0 인 경우는 stationary 데이터로 판단됩니다.
예를 들어, 아래의 그래프는 stationary 데이터가 아닙니다. 평균이 시간의 흐름에 따라 일정하지 않다는 것에 주목하세요.
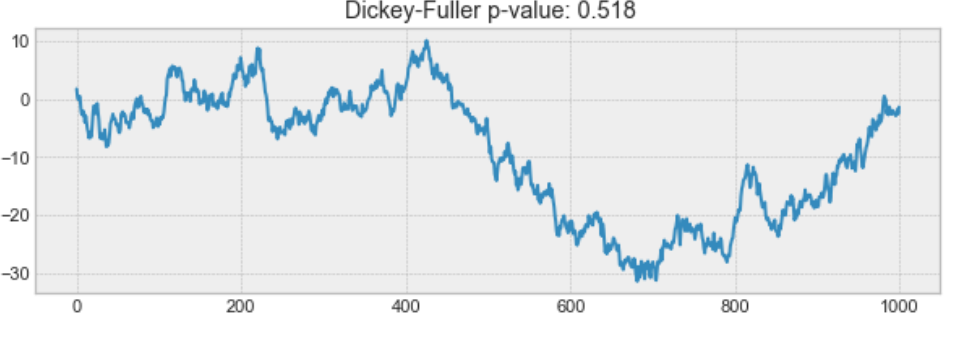 Example of a non-stationary process
Example of a non-stationary process
Modelling time series
예측을 위해 시계열 데이터를 모델링 하는 것은 많은 방법들이 있고, 여기서는 아래의 방법들을 소개하려고 합니다.
- moving average
- exponential smoothing
- ARIMA
Moving average (MA)
Moving average model은 아마도 시계열 데이터 모델링에서 가장 나이브한 접근 방식일 것입니다. 모델은 단순히 다음 단계의 예측 값을 과거에 관측한 모든 값들의 평균으로 계산합니다.
간단하지만, 이 모델은 놀라울정도로 좋은 성능을 낼 수도 있으며 좋은 출발점이 될 수 있습니다.
반면, moving average는 데이터에서 흥미로운 트렌트를 식별하는데 사용될 수 있습니다. 우리는 moving average 모델을 적용할 window를 정의하여 시계열 데이터를 부드럽게(smoothing) 할 수 있고, 서로 다른 트렌드들에 대해 강조할 수 있습니다.
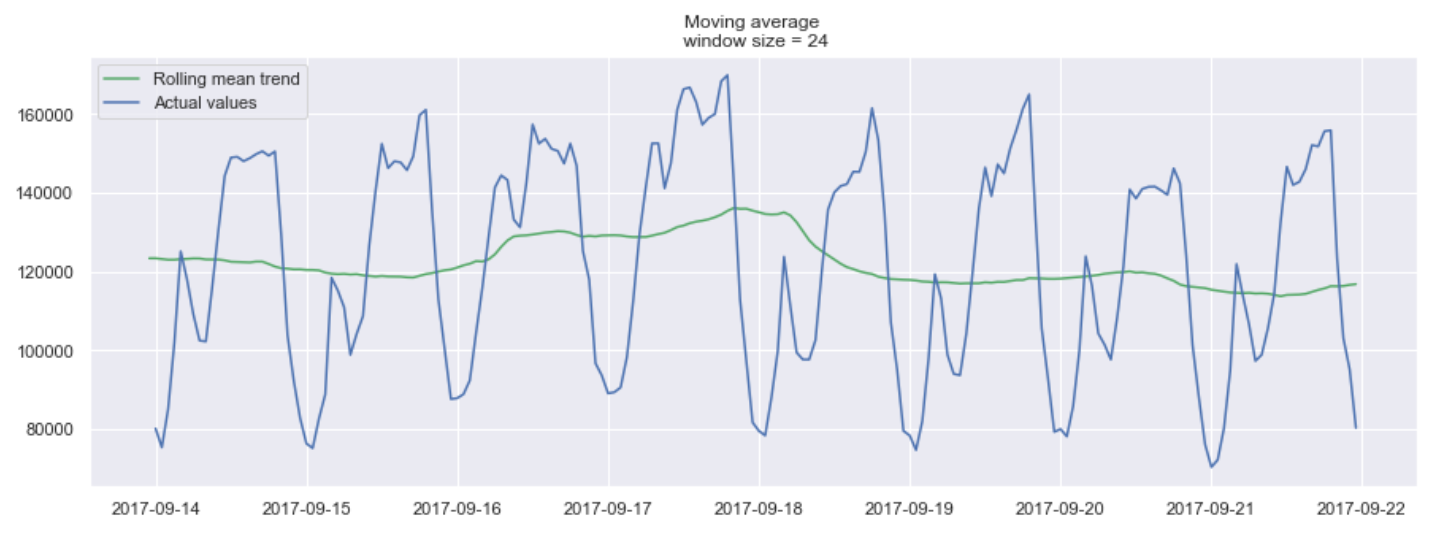 24시간 단위의 window를 가진 moving average 예시
24시간 단위의 window를 가진 moving average 예시
위의 그래프에서, 우리는 24시간 단위의 moving average 모델을 적용했습니다. 초록색 선은 시계열 데이터를 부드럽게 했고, 24시간의 기간동안 2개의 최고점이 있는 것을 확인 할 수 있습니다.
물론, window를 길게할 수록 트렌드는 더 부드러워 질 것입니다. 아래는 더 작은 window로 moving average를 적용한 예시입니다.
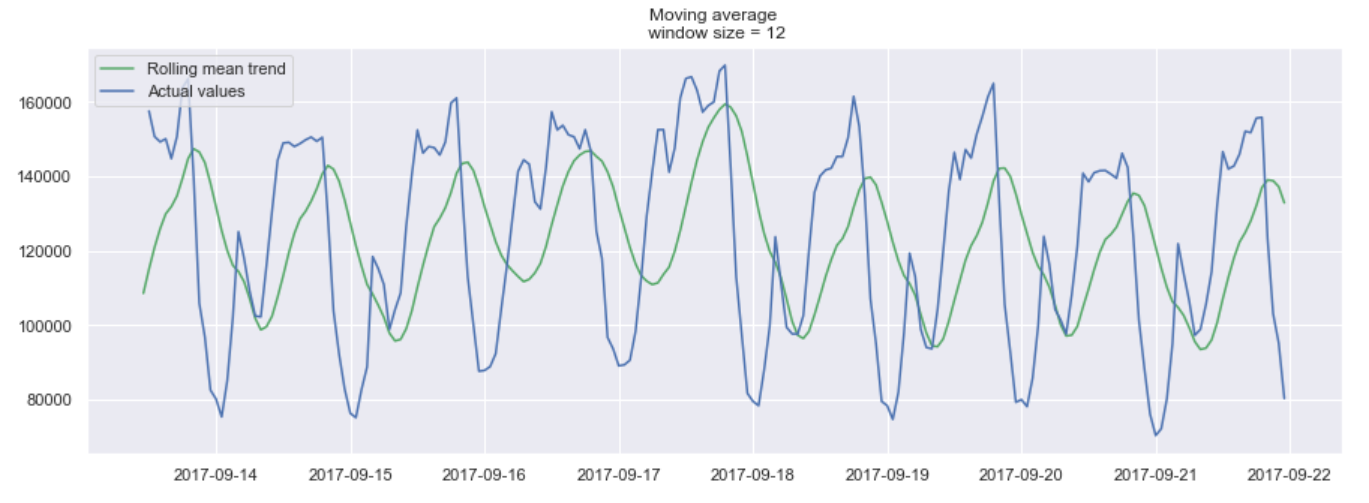 12시간 단위의 window를 가진 moving average 예시
12시간 단위의 window를 가진 moving average 예시
Exponential smoothing
Exponential smoothing 는 moving average와 비슷한 로직을 사용하지만, 이번에는, 각 관측치마다 다른 가중치(weight)를 적용합니다. 즉, 우리가 현재로부터 더 멀리 이동함에 따라 관측치에 더 적은 중요도를 매깁니다.
수학적으로, exponential smoothing 은 다음과 같이 나타낼 수 있습니다.
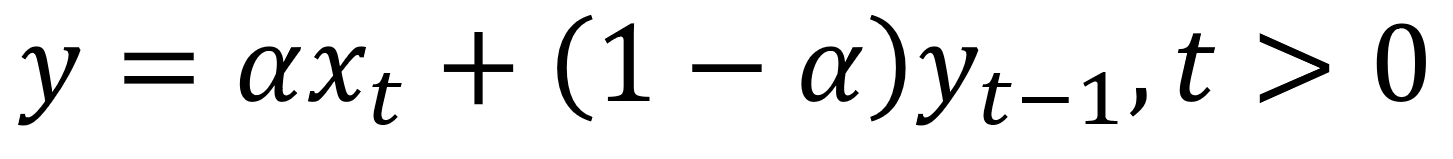 Exponential smoothing expression
Exponential smoothing expression
여기서, alpha값은 0 과 1 사이의 값을 가지는 smoothing factor 입니다. 이 alpha값은 시간이 지남에 따라 얼마나 가중치가 빠르게 감소하는지를 결정합니다.
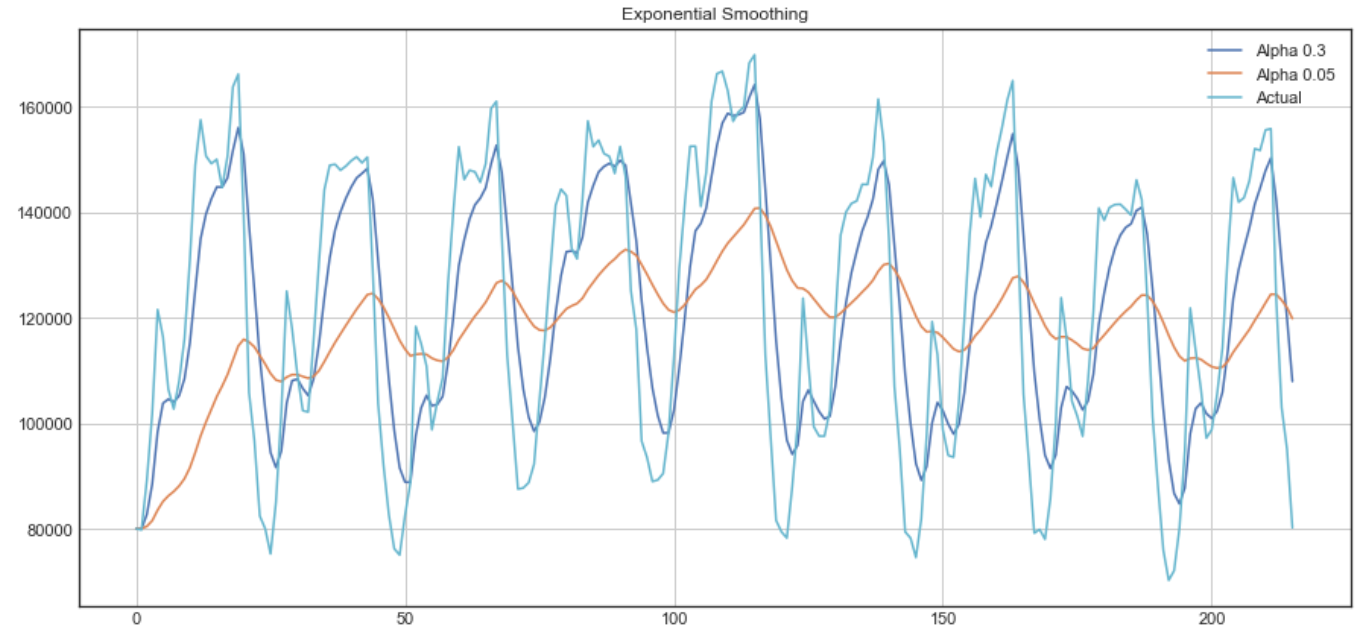 Exponential smoothing의 예시
Exponential smoothing의 예시
위의 그래프에서, 짙은 파란색 선이 0.3의 smoothing factor를 가지는 exponential smoothing를 적용한 결과이고, 주황색 선이 0.05의 smoothing factor를 가지는 exponential smoothing 결과 입니다.
보시다시피, smoothing factor가 작아질수록, 시계열 데이터가 더 부드러워집니다. 이는 smoothing factor가 0에 가까워질 수록 moving average model에 가까워지기 때문에 의미가 있습니다.
Double exponential smoothing
시계열 데이터에 trend가 존재할 경우에는 Double exponential smoothing을 사용합니다. 이 경우, 우리는 단순히 exponential smoothing 을 재귀적으로 두 번 적용하는 방식을 사용합니다.
수학적표현:
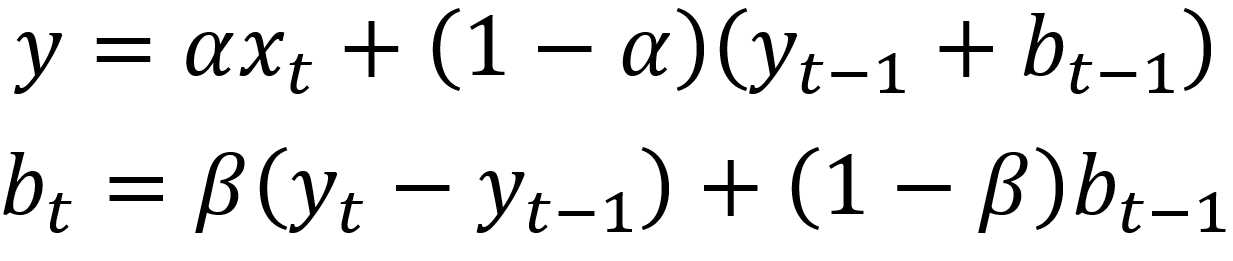
여기서 beta 값은 trend smoothing factor로, 0 과 1 사이의 값을 가집니다.
아래에서 서로 다른 alpha와 bets 값들이 시계열 데이터의 형태에 어떻게 영향을 미치는지 확인할 수 있습니다.
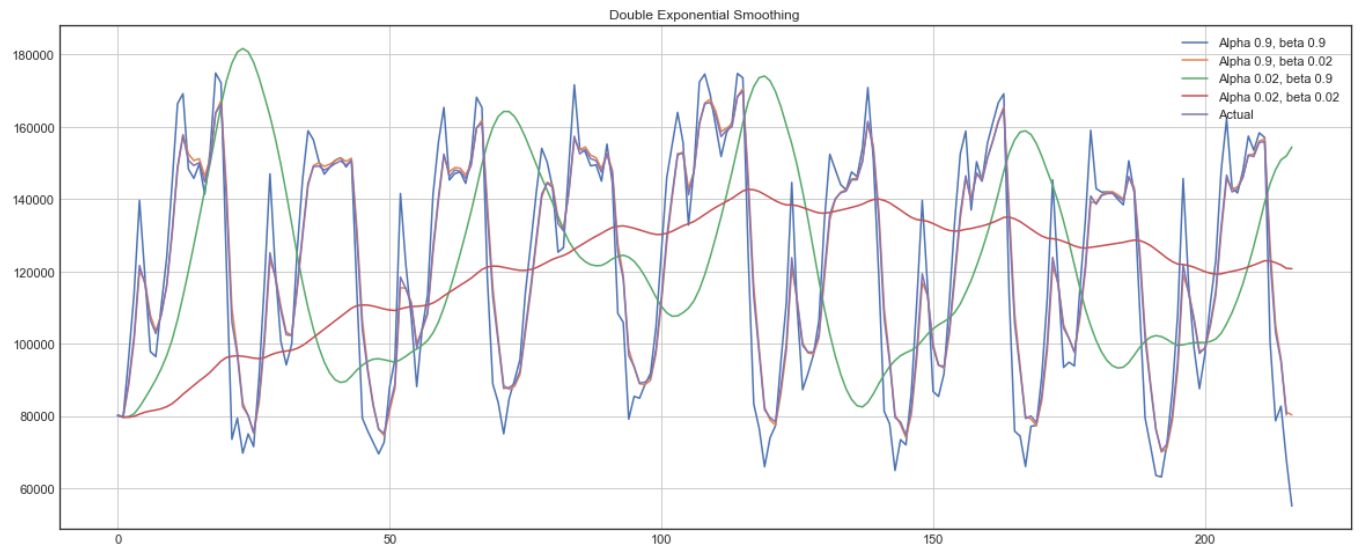 Double exponential smoothing 의 예
Double exponential smoothing 의 예
Triple exponential smoothing
이 방법은 seasonal smoothing factor을 더하여, double exponential smoothing을 확장한 방법입니다. 물론, 이 방법은 시계열 데이터에서 seasonality를 발견했을 때 유용합니다.
수학적으로, triple exponential smoothing 은 다음과 같이 표현됩니다.
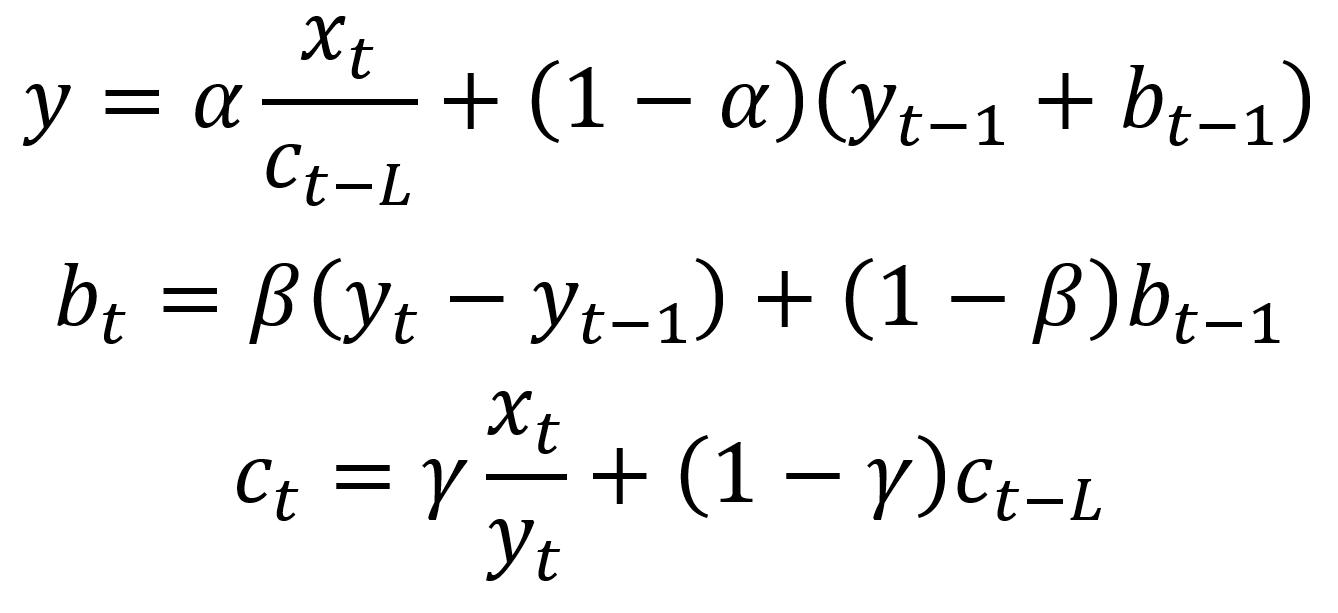
위에서 gamma 값은 seasonal smoothing factor 이며, L 은 season의 길이를 나타냅니다.
Seasonal autoregressive integraded moving average model (SARIMA)
SARIMA는 실제로 non-stationary 속성과 seasonality를 가진 시계열 데이터에 대한 복잡한 모델을 만들 수 있는 간단한 모델들의 조합입니다.
맨 처음, autoregression model AR(p)에서 시작합니다. 이 모델은 기본적으로 시계열 데이터 그 자체에 대한 regression입니다. 여기서 우리는 현재 값이 약간의 시간 지연을 가지고 과거의 값들에 대해 의존성이 있다고 가정합니다. 여기서 p는 모델의 차수를 의미합니다. AR(1)의 경우 가장 간단한 모델로, 바로 직전 데이터가 다음 데이터에 영향을 준다고 가정한 모델입니다.
AR(p)의 수학적 표현:
그리고, 우리는 moving average model MA(q)을 추가합니다. MA(q)는 q차 moving average model 입니다.
MA(q)의 수학적 표현:
(여기까지가 ARMA(p, q) 모델입니다.)
그리고, 우리는 integeration I(d)을 추가합니다. 여기서 d 값은 시계열 데이터를 stationary로 변형하기 위해 필요한 차분(difference) 의 개수입니다.
(시계열 𝑌𝑡 을 차분(difference)한 결과로 만들어진 시계열 ∇𝑌𝑡=𝑌𝑡−𝑌𝑡−1 이 ARMA 모형을 따르면 원래의 시계열 𝑌𝑡를 ARIMA(Autoregressive Integrated Moving Average) 모형이라고 합니다.)
최종적으로 우리는 seasonality S(P, D, Q, s) 요소를 추가합니다. 여기서 s는 단순히 season의 길이입니다. 더욱이, 이 요소는 앞선 p와 q와 같은 값을 가지는 파라미터 P와 Q를 사용합니다. D는 seasonal integration의 차수로 seasonality를 제거하기 위한 차분 값의 개수입니다.
모델을 모두 종합하여 우리는 SARIMA(p, d, q)(P, D, Q, s) 모델을 얻습니다.
가장 중요한 것은, SARIMA로 모델링 하기 전에 반드시 우리의 시계열 데이터에서 seasonality와 non-stationary 패턴을 제거하기 위해 변형해야 한다는 것 입니다.
이것이 시계열에 대한 모든 것 입니다. 이보다 더 많은 내용들이 있지만, 이 글은 나중의 탐구를 위한 좋은 출발점입니다.

